موارد استفاده مدل یابی معادلات ساختاری، اصلاحات و مفروضه های آن
موارد استفاده مدل یابی معادلات ساختاری
مدل یابی معادلات ساختاری را می توان در جهت مقاصد پژوهشی ذیل به کار برد:
1- مدل یابی علی یا تحلیل مسیر:
پارامترهای حاصل از تحلیل رگرسیون دست کم در سه موقعیت اساسی زیر نمی تواند اطلاعات لازم را فراهم آورد:
وقتی متغیرهای مشاهده شده حاوی خطاهای اندازه گیری و بین متغیرهای واقعی روابط جالب و بدون تورش وجود داشته باشد.
وقیت بین متغیرهای مشاهده شده روابط درهم تنیده جریان علی وجود داشته باشد.
وقتی متغیرهای مهم تبیین شده مشاهده نشده باشد.
اما توابع ساختاری می تواند در همه موقعیت های بالا نقش مهم و سازنده ای ایفا کند. علوم اجتماعی و رفتاری بر خلاف علوم طبیعی، به ندرت به تجزیه و تحلیل دقیق در شرایط کنترل شده دستیابی دارد. در این علوم، استنباط روابط علی بر پایه مطالعاتی صورت می گیرد که در آنها مدل ها و در قالب سازه های نظری که مستقیما مشاهده پذیر و اندازه پذیر نیست، بیان می شود. اما برای عملیاتی کردن و اندازه گیری متغیرهای نظری می توان از شاخص ها یا نشانه هایی که نشانگر نامیده می شود، استفاده کرد. استنباط های علی به واقع به مسیرهایی بستگی دارد که طرح مطالعه مشخص کرده است.
2- تحلیل عاملی تاییدی:
این روش که به واقع بسط تحلیل عاملی معمولی است، یکی از جنبه های مهم SEM است، که در آن فرضیه های معینی درباره ساختارهای بارهای عاملی و همبستگی های متقابل بین متغیرها مورد آزمون قرار می گیرد. از لحاظ سنتی، تحلیل عاملی با آشکار ساختن ابعاد زیربنایی یا واریانس عامل مشترک در مجموعه ای از پرسش ها یا سوال های تستی سروکار دارد.
برای معرفی یک سازه نظری، معمولا مجموعه ای از پرسش ها تهیه می شود و تحلیل عاملی به تدوین شاخصی که در پژوهش به کار می رود، کمک خواهد کرد. برای معرفی ابعاد زیربنایی سازه مورد نظر، تحلیل عاملی می تواند یک یا چند عامل را آشکار سازد. برپایه نتایج تحلیل عاملی می توان گفت که یک سازه، تک بعدی یا چندبعدی است.
به این رویکرد، در حال حاضر، به سبب آنکه دارای ماهیت اکتشافی است و نه ماهیت آزمون فرضیه، تحلیل عاملی اکتشافی گفته می شود. عامل چون در تحلیل عاملی مشاهده ناپذیر است، متغیر مکنون خوانده می شود، که در تحلیل عاملی، پیش بینی کننده پاسخ ها در متغیرهای اندازه گرفته شده و مشاهده شده است، به واقع، روایی یک تحلیل عاملی تا حدودی از طریق تعیین این مطلب مشخص می شود که عامل ها با چه دقتی واریانس موجود در پرسش های انفرادی را توجیه می کنند. یعنی، چقدر از واریانس موجود در پرسش ها با عامل ها اشتراک دارد.
مدلی یابی معادله ساختاری، علاوه بر تحلیل اکتشافی، تحلیل عاملی تاییدی را نیز به کار می برد. این تحلیل اساسا یک روش آزمون فرضیه است، و بر این مفروضه متکی است که شما درباره اینکه مولفه متغیرهای مکنون چیست اندیشه ای دارید؛یعنی به دنبال یافتن نشانگرها نیستید. SEM این مطلب را که آیا نشانگرهایی که برای معرفی سازه یا متغیر مکنون خود برگزیده اید، واقعا معرف آن است یا نه، می آزماید و گزارش می دهد که نشانگرهای انتخابی با چه دقتی معرف یا برازنده متغیرمکنون است. برای بهبود برازندگی، نشانگرها با متغیر مکنون نیز راه هایی پیشنهاد می کنند.
3- تحلیل عاملی مرتبه دوم:
صورتی از تحلیل عاملی است که در آن خود ماتریس همبستگی عامل های مشترک تحلیل می شود تا عامل های مرتبه دوم به دست آید.
4- مدل های مختلف رگرسیون:
بسط تحلیل رگرسیون خطی که در آن وزن هایی رگرسیون ممکن است مقید به تساوی با یکدیگر باشد، یا برابر با مقادیر عددی معینی قرار داده شود. SEM مقایسه ضرایب رگرسیون، واریانس ها، میانگین ها حتی با گروه های بین آزمودنی ها چندگانه را به گونه هم زمان امکان پذیر می سازد.
5- مدل های ساختاری کوواریانس:
این فرضیه را که یک ماتریس کوواریانس دارای شکل به خصوصی است آزمون می کند. برای مثال، می توانید این فرضیه را که مجموعه ای از متغیرها دارای واریانس های برابر هستند بیازمایید.
6- مدل های ساختاری همبستگی:
این فرضیه را که یک ماتریس همبستگی دارای شکل به خصوصی است آزمون می کند. برای مثال، می توانید این فرضیه کلاسیک را که ماتریس همبستگی دارای ساختار دوری است، بیازمایید.
اصطلاحات مدل یابی ساختاری:
مدل یابی معادلات ساختاری بر پایه فرضیه هایی درباره وجود روابط علی بین متغیرها، مدل های علی را با دستگاه معادله خطی آزمون می کند. بدین ترتیب، SEM، روابط نظری بین شرایط ساختاری معین و مفروض را می آزماید و برآورد روابط علی میان متغیرهای مکنون (مشاهده نشده) و نیز روابط میان متغیرهای اندازه گیری شده (مشاهده شده) را امکان پذیر می سازد.
متغیرهای مستقل که فرض بر آن است بدون خطا اندازه گیری می شوند، متغیرهای برونزا یا جریان دهنده و متغیرهای وابسته یا میانجی متغیرهای درونزا یا جریان گیرنده نامیده می شوند. متغیرهای آشکار آشکار یا مشاهده شده به گونه مستقیم به وسیله پژوهشگر اندازه گیری می شود، در حالی که متغیرهای مکنون یا مشاهده نشده به گونه مستقیم اندازه گیری نمی شود، بلکه بر اساس روابط یا همبستگی های بین متغیرهای اندازه گیری شده استنباط می شوند. این برآورد آماری به همان طریق که یک تحلیل عاملی اکتشافی حضور عامل های مکنون را از واریانس مشترک بین متغیرهای مشاهده شده استنباط می کند، به دست می آید.
بنابر آنچه گفته شد، مدل معادله ساختاری شامل دو مؤلفه است: مدل اندازه گیری که در آن متغیرهای مکنون پیشنهاد و از طریق تحلیل عاملی تاییدی آزمون می شود و مدل ساختاری که در آن متغیرهای مکنون و نیز متغیرهای مشاهده شده ای که نشانگر متغیرهای مکنون است از یک راه منطقی با هم مرتبط می شود.
کاربران SEM روابط میان متغیرهای مشاهده شده و مشاهده نشده را با استفاده از نمودار مسیر نشان می دهند. این نمودار که نقش اساسی در مدل یابی ساختاری بازی می کند، مانند فلوچارت های رایانه ای است، که متغیرهایی را که با خطوط بیانگر جریان علی باهم متصل شده اند، نشان می دهد. نمودار مسیر را می توان به عنوان وسیله ای برای نمایش این مطلب در نظر گرفت که کدام متغیرها موجب تغییراتی در متغیرهای دیگر می شود. همه متغیرهای مستقل دارای پیکان هایی اند که به سوی متغیر وابسته نشانه می روند. ضریب وزنی بالای پیکان قرار می گیرد.
مفروضه های مدل معادله ساختاری:
مدل یابی معادله ساختاری، بسط انعطاف پذیر و قدرتمند مدل خطی کلی است، و بنابراین مانند هر روش آماری، دارای شماری از مفروضه هاست که باید صادق بوده یا دست کم به گونه تقریب برقرار باشد، تا نسبت به نتایج آن اطمینان حاصل شود. دو مسئله اساسی، یعنی حجم گروه نمونه و کار با داده های گمشده می باشد.
حجم منطقی گروه نمونه:
بر پایه پیشنهاد جمیز استیونس در نظر گرفتن پانزده مورد برای هر متغیر پیش بین در تحلیل رگرسیون چندگانه با روش معمولی کمترین مجذورات استاندارد، یک قاعده سرانگشتی خوب به شمار می آید. چون SEM در برخی جنبه ها کاملا مرتبط با رگرسیون چند متغیری است، تعداد 15 مورد به ازای هر متغیر اندازه گیری شده در SEM غیر منطقی نیست.
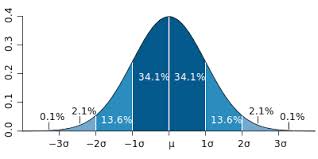
لوهلین نتایج مطالعات مشابه مونت کارلو را با استفاده از مدل های تحلیل عاملی تاییدی گزارش کرده و پس از بررسی پیشینه های پژوهش نتیجه می گیرد که برای این طبقه از مدل ها با دو یا چهار عامل، پژوهشگر باید روی گردآوری دست کم 100 مورد یا بیش از آن 200 مورد برنامه ریزی کند. کاربرد نمونه های کوچکتر می تواند موجب عدم حصول همگرایی، به دست آمدن جواب های نامناسب و یا دقت پایین برآورد پارامترها و به ویژه خطاهای استاندارد شود. خطای استاندارد برنامهSEM بر پایه مفروضه نمونه های بزرگ محاسبه می شود. زمانی که توزیع داده ها نرمال نبوده یا کجی داشته باشد، گروه های نمونه با حجم بزرگتر مورد نیاز است. پیشنهاد کلی آن است که تا حد امکان داده های بیشتری به دست آورید.
داده های کامل یا کاربرد مناسب داده های ناکافی:
چنانچه برای تحلیل، از داده های ورودی خام استفاده شود، این داده ها باید کامل و بدون مقادیر گمشده باشند. برای کار با داده های ناکامل، چندین راه حل پیش تجربی وجود دارد. حذف لیستی که در آن همه نمره های مربوط به داده های گمشده حذف می شود و حذف زوجی که در آن همبستگی دو متغیری فقط برای مواردی که داده های آن کامل وجود دارد محاسبه می شود، از راه حل های متداول برای کار با مقادیر گمشده است. روش دیگر پیش تجربی برای داده گمشده، جایگزین ساختن این داده ها با میانگین متغیر مربوط است.
تدوین مدل:
مدل، به گونه ساده یک گزاره آماری درباره روابط میان متغیرهاست. تحلیل مسیر مثال خوبی برای مدل، و تدوین مدل، تمرینی برای بیان رسمی می کمدل است. ترجمه مشهود و آشکار نظریه به صورت معادلات ریاضی انجام می پذیرد. این مدل از طریق نمایش متغیرهای مستقل و وابسته به ترسیم نمودار مسیر کمک می کند. متغیرهای مستقل اغلب متغیرهای برونزا خوانده می شود، یعنی علل آنها خارج از مدل تعیین می گردد. متغیرهای وابسته اغلب متغیرهای درونزا خوانده می شود، زیرا فرض می شود که علت آنها از درون مدل تعیین می شود.
تدوین مدل در SEM، گام عمده ای است که در فرایند آن باید سازه های مربوط، مکنون و مشاهده شده و روابط بین سازه ها مشخص گردد. در مدل باید اصل اقتصاد و صرفه جویی نیز رعایت شود، و ضرورتی ندارد که شمامل هر متغیر علی ممکن باشد. گنجانیدن سازه های بیش از اندازه در مدل می توند موجب آزمون ناپذیری آن شود، و اگر سازه های مهمی را حذف کنید، خطر تولید یک مدل نامناسب کاذب را به جان خریده اید. نکته مهم آن است که مدل شما باید اندیشه ها و مفاهیم نظری مورد علاقه شما را به خوبی منعکس سازد.
تجربه نشان داده است که به سادگی نمی توانید تنها به خاطر آنکه چیزی را ببینید یک مدل را به کار ببرید، بلکه باید نظریه خوبی در دست داشته باشید. عمل تدوین مدل، انتخاب نشانگرها برای متغیرهای مکنون را نیز در بر می گیرد. به عنوان یک قاعده کلی، برای یک سازه مکنون، باید نشانگرهای چندگانه داشته باشید. این موضوع هم دلیل منطقی و هم دلیل آماری دارد. یک سازه پیچیده وقتی از طریق نشانگرهای چندگانه تسخیر شود، معتبرتر و رواتر است. برای هر متغیر مکنون سه نشانگر یا بیشتر توصیه می شود.
تدوین مدل شامل فرمول بندی گزاره هایی درباره پارامترها نیز می باشد. پارامتر ضریب عددی است که رابطه بین سازه ها را توصیف می کند. تعیین پارامترها این مطلب را که روابط دارای یک جهت یا چند جهت است یا نه نیز شامل می شود.